Triangle With 2 Congruent Sides

Right triangle with a feature making calculations on the triangle easier

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas be. For example, a right triangle may have angles that form simple relationships, such every bit 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is 1 in which the lengths of the sides form ratios of whole numbers, such as three : 4 : 5, or of other special numbers such as the gilt ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate diverse lengths in geometric bug without resorting to more avant-garde methods.

Angle-based [edit]

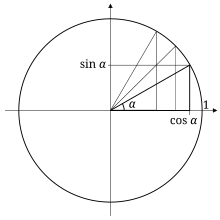
Special angle-based triangles inscribed in a unit circumvolve are handy for visualizing and remembering trigonometric functions of multiples of 30 and 45 degrees.

"Angle-based" special right triangles are specified by the relationships of the angles of which the triangle is equanimous. The angles of these triangles are such that the larger (right) bending, which is 90 degrees or $π$ / 2 radians, is equal to the sum of the other two angles.

The side lengths are generally deduced from the basis of the unit circle or other geometric methods. This arroyo may be used to rapidly reproduce the values of trigonometric functions for the angles 30°, 45°, and 60°.

Special triangles are used to aid in calculating mutual trigonometric functions, as below:

degrees	radians	gons	turns	sin	cos	tan	cotan
0°	0	0^chiliad	0	√0 / 2 = 0	√4 / 2 = ane	0	undefined
30°	$π$ / 6	33+ 1 / 3 ^thou	1 / 12	√1 / two = i / two	√3 / two	1 / √3	√three
45°	$π$ / 4	50^chiliad	1 / 8	√2 / two = 1 / √ii	√2 / 2 = 1 / √2	one	i
60°	$π$ / three	66+ ii / three ^g	1 / six	√3 / 2	√1 / 2 = 1 / ii	√3	1 / √iii
90°	$π$ / 2	100^thou	1 / iv	√4 / 2 = 1	√0 / 2 = 0	undefined	0

45°–45°–90°

30°–60°–xc°

The 45°–45°–90° triangle, the thirty°–60°–90° triangle, and the equilateral/equiangular (60°–60°–lx°) triangle are the 3 Möbius triangles in the aeroplane, significant that they tessellate the plane via reflections in their sides; see Triangle grouping.

45°–45°–xc° triangle [edit]

The side lengths of a 45°–45°–xc° triangle

In plane geometry, amalgam the diagonal of a square results in a triangle whose three angles are in the ratio 1 : 1 : 2, calculation up to 180° or $π$ radians. Hence, the angles respectively measure 45° ( $π$ / four ), 45° ( $π$ / 4 ), and ninety° ( $π$ / 2 ). The sides in this triangle are in the ratio 1 : 1 :√2 , which follows immediately from the Pythagorean theorem.

Of all right triangles, the 45°–45°–90° degree triangle has the smallest ratio of the hypotenuse to the sum of the legs, namely √2 / 2 .^[i] ^{: p.282, p.358} and the greatest ratio of the altitude from the hypotenuse to the sum of the legs, namely √ii / 4 .^[1] ^: p.282

Triangles with these angles are the merely possible right triangles that are too isosceles triangles in Euclidean geometry. However, in spherical geometry and hyperbolic geometry, there are infinitely many different shapes of correct isosceles triangles.

30°–60°–90° triangle [edit]

The side lengths of a xxx°–threescore°–90° triangle

This is a triangle whose 3 angles are in the ratio 1 : 2 : three and respectively measure xxx° ( $π$ / six ), threescore° ( $π$ / 3 ), and 90° ( $π$ / 2 ). The sides are in the ratio 1 :√three : 2.

The proof of this fact is clear using trigonometry. The geometric proof is:

Depict an equilateral triangle ABC with side length two and with point D as the midpoint of segment BC. Draw an altitude line from A to D. Then ABD is a thirty°–60°–ninety° triangle with hypotenuse of length 2, and base BD of length 1.

The fact that the remaining leg AD has length √3 follows immediately from the Pythagorean theorem.

The 30°–60°–90° triangle is the just correct triangle whose angles are in an arithmetic progression. The proof of this fact is simple and follows on from the fact that if α, α + δ , α + 2δ are the angles in the progression then the sum of the angles 3α + 3δ = 180°. After dividing by three, the angle α + δ must be 60°. The right bending is 90°, leaving the remaining angle to be 30°.

Side-based [edit]

Right triangles whose sides are of integer lengths, with the sides collectively known as Pythagorean triples, possess angles that cannot all be rational numbers of degrees.^[2] (This follows from Niven's theorem.) They are nigh useful in that they may be easily remembered and whatever multiple of the sides produces the same relationship. Using Euclid's formula for generating Pythagorean triples, the sides must be in the ratio

chiliad ^two − n ² : 2mn : m ^two + n ²

where m and n are whatever positive integers such that m > n .

Mutual Pythagorean triples [edit]

In that location are several Pythagorean triples which are well-known, including those with sides in the ratios:

3:	4	:5
5:	12	:13
8:	15	:17
7:	24	:25
9:	40	:41

The 3 : iv : 5 triangles are the only right triangles with edges in arithmetics progression. Triangles based on Pythagorean triples are Heronian, meaning they have integer area as well equally integer sides.

The possible use of the three : four : v triangle in Ancient Egypt, with the supposed use of a knotted rope to lay out such a triangle, and the question whether Pythagoras' theorem was known at that time, have been much debated.^[3] It was beginning conjectured by the historian Moritz Cantor in 1882.^[iii] It is known that right angles were laid out accurately in Ancient Egypt; that their surveyors did employ ropes for measurement;^[3] that Plutarch recorded in Isis and Osiris (around 100 AD) that the Egyptians admired the iii : four : five triangle;^[3] and that the Berlin Papyrus 6619 from the Middle Kingdom of Egypt (earlier 1700 BC) stated that "the area of a square of 100 is equal to that of two smaller squares. The side of one is ½ + ¼ the side of the other."^[4] The historian of mathematics Roger L. Cooke observes that "It is hard to imagine anyone being interested in such conditions without knowing the Pythagorean theorem."^[3] Against this, Cooke notes that no Egyptian text earlier 300 BC actually mentions the employ of the theorem to find the length of a triangle's sides, and that there are simpler ways to construct a right angle. Cooke concludes that Cantor's conjecture remains uncertain: he guesses that the Ancient Egyptians probably did know the Pythagorean theorem, but that "there is no evidence that they used it to construct correct angles".^[3]

The post-obit are all the Pythagorean triple ratios expressed in everyman course (beyond the five smallest ones in everyman form in the list above) with both non-hypotenuse sides less than 256:

11:	60	:61
12:	35	:37
thirteen:	84	:85
15:	112	:113
sixteen:	63	:65
17:	144	:145
19:	180	:181
twenty:	21	:29
20:	99	:101
21:	220	:221

24:	143	:145
28:	45	:53
28:	195	:197
32:	255	:257
33:	56	:65
36:	77	:85
39:	80	:89
44:	117	:125
48:	55	:73
51:	140	:149

52:	165	:173
57:	176	:185
60:	91	:109
60:	221	:229
65:	72	:97
84:	187	:205
85:	132	:157
88:	105	:137
95:	168	:193
96:	247	:265

104:	153	:185
105:	208	:233
115:	252	:277
119:	120	:169
120:	209	:241
133:	156	:205
140:	171	:221
160:	231	:281
161:	240	:289
204:	253	:325
207:	224	:305

Almost-isosceles Pythagorean triples [edit]

Isosceles right-angled triangles cannot have sides with integer values, because the ratio of the hypotenuse to either other side is √2 and √2 cannot be expressed as a ratio of two integers. Even so, infinitely many virtually-isosceles right triangles do exist. These are correct-angled triangles with integer sides for which the lengths of the not-hypotenuse edges differ by i.^[v] ^[6] Such almost-isosceles right-angled triangles tin be obtained recursively,

a ₀ = 1, b ₀ = 2

a _north = 2b _n−1 + a _n−one

b _{due north} = iia _{due north} + b _{due north−1}

a _northward is length of hypotenuse, n = ane, 2, 3, .... Equivalently,

({\tfrac {x-1}{2}})^{2}+({\tfrac {x+1}{ii}})^{ii}=y^{ii}

where {x, y} are solutions to the Pell equation x ² − twoy ² = −1, with the hypotenuse y being the odd terms of the Pell numbers 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378... (sequence A000129 in the OEIS).. The smallest Pythagorean triples resulting are:^[vii]

3 :	4	: five
xx :	21	: 29
119 :	120	: 169
696 :	697	: 985
4,059 :	4,060	: 5,741
23,660 :	23,661	: 33,461
137,903 :	137,904	: 195,025
803,760 :	803,761	: 1,136,689
iv,684,659 :	four,684,660	: six,625,109

Alternatively, the same triangles can be derived from the foursquare triangular numbers.^[eight]

Arithmetic and geometric progressions [edit]

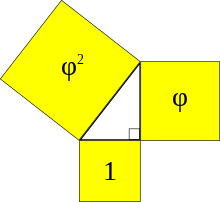
A Kepler triangle is a right triangle formed by three squares with areas in geometric progression according to the golden ratio.

The Kepler triangle is a right triangle whose sides are in geometric progression. If the sides are formed from the geometric progression a, ar, ar ² then its common ratio r is given by r = √ φ where φ is the gilt ratio. Its sides are therefore in the ratio ane : √ φ : φ . Thus, the shape of the Kepler triangle is uniquely adamant (upwardly to a scale factor) past the requirement that its sides be in geometric progression.

The 3–4–v triangle is the unique correct triangle (upwards to scaling) whose sides are in arithmetic progression.^[9]

Sides of regular polygons [edit]

The sides of a pentagon, hexagon, and decagon, inscribed in congruent circles, form a correct triangle

Let

a=2\sin {\frac {\pi }{10}}={\frac {-one+{\sqrt {five}}}{two}}={\frac {1}{\varphi }}\approx 0.618

exist the side length of a regular decagon inscribed in the unit circle, where $\varphi$ is the gilt ratio. Let

b=2\sin {\frac {\pi }{6}}=1

be the side length of a regular hexagon in the unit circle, and let

c=2\sin {\frac {\pi }{5}}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1.176

exist the side length of a regular pentagon in the unit circle. Then $a^{2}+b^{2}=c^{ii}$ , and then these three lengths form the sides of a right triangle.^[10] The same triangle forms one-half of a golden rectangle. It may too be found inside a regular icosahedron of side length $c$ : the shortest line segment from any vertex $5$ to the plane of its five neighbors has length $a$ , and the endpoints of this line segment together with any of the neighbors of $V$ form the vertices of a right triangle with sides $a$ , $b$ , and $c$ .^[11]

References [edit]

^ ^a ^b Posamentier, Alfred S., and Lehman, Ingmar. The Secrets of Triangles. Prometheus Books, 2012.
^ Weisstein, Eric W. "Rational Triangle". MathWorld.
^ ^a ^b ^c ^d ^e ^f Cooke, Roger Fifty. (2011). The History of Mathematics: A Brief Course (2nd ed.). John Wiley & Sons. pp. 237–238. ISBN978-1-118-03024-0.
^ Gillings, Richard J. (1982). Mathematics in the Fourth dimension of the Pharaohs . Dover. p. 161.
^ Forget, T. W.; Larkin, T. A. (1968), "Pythagorean triads of the form x, x + 1, z described past recurrence sequences" (PDF), Fibonacci Quarterly, half dozen (3): 94–104 .
^ Chen, C. C.; Peng, T. A. (1995), "Almost-isosceles correct-angled triangles" (PDF), The Australasian Periodical of Combinatorics, 11: 263–267, MR 1327342 .
^ (sequence A001652 in the OEIS)
^ Nyblom, M. A. (1998), "A note on the set up of almost-isosceles right-angled triangles" (PDF), The Fibonacci Quarterly, 36 (4): 319–322, MR 1640364 .
^ Beauregard, Raymond A.; Suryanarayan, East. R. (1997), "Arithmetics triangles", Mathematics Mag, 70 (2): 105–115, doi:10.2307/2691431, MR 1448883 .
^ Euclid's Elements, Book Xiii, Proposition x.
^ nLab: pentagon decagon hexagon identity.

External links [edit]

3 : four : 5 triangle
30–60–90 triangle
45–45–ninety triangle – with interactive animations